5. 最长回文子串

#leetcode/palindrome #leetcode/unsolved #leetcode/dp #leetcode/sub/consecutive

5. 最长回文子串

Similar Question

leading to the advanced question

Solution Tips

方案一: 中心扩展法

/**
 * @param {string} s
 * @return {string}
 */
var longestPalindrome = function(s) {
        if (s.length<2){
            return s
        }
        let res = ''
        for (let i = 0; i < s.length; i++) {
            // 回文子串长度是奇数
            helper(i, i)
            // 回文子串长度是偶数
            helper(i, i + 1) 
        }

        function helper(m, n) {
            while (m >= 0 && n < s.length && s[m] == s[n]) {
                m--
                n++
            }
            // 注意此处m,n的值循环完后  是恰好不满足循环条件的时刻
            // 此时m到n的距离为n-m+1，但是mn两个边界不能取 所以应该取m+1到n-1的区间  长度是n-m-1
            if (n - m - 1 > res.length) {
                // slice也要取[m+1,n-1]这个区间 
                res = s.slice(m + 1, n)
            }
        }
        return res
};

方案二: 基于中心扩展法的动态规划

public class Solution {

    public String longestPalindrome(String s) {
        int len = s.length();
        if (len < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        boolean[][] dp = new boolean[len][len];
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < len; i++) {
            dp[i][i] = true;
        }

        char[] charArray = s.toCharArray();
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= len; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < len; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= len) {
                    break;
                }

                if (charArray[i] != charArray[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substring(begin, begin + maxLen);
    }
}

方案三: 最长公共子串

反转字符串，找到最长的公共子串，判断是否是回文串，否则继续判断第二长的公共子串，判断是否是回文串

这似乎是可行的，让我们看看下面的一些例子。

当 S 的其他部分中存在非回文子串的反向副本时，最长公共子串法就会失败。

我们还需要判断该字符串倒置前的下标和当前的字符串下标是不是匹配。

分析实例

比如 S="caba"，S'="abac" ，S’ 中 aba 的下标是 0 1 2 ，倒置前是 3 2 1，和 S 中 aba 的下标符合，所以 aba 就是我们需要找的。当然我们不需要每个字符都判断，我们只需要判断末尾字符就可以。

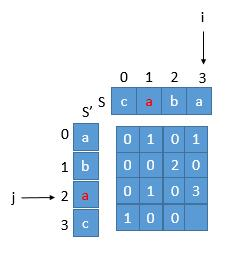
image.png

首先 i，j 始终指向子串的末尾字符。所以 j 指向的红色的 a 倒置前的下标是 beforeRev = length-1-j=4-1-2=1，对应的是字符串首位的下标，我们还需要加上公共字符串的长度才是末尾字符的下标，也就是 beforeRev+arr[i][j]-1=1+3-1=3，因为 arr[i][j] 保存的就是当前子串的长度，也就是图中的数字 3。此时再和它与 i 比较，如果相等，则说明它是我们要找的回文串。

实现

 var longestPalindrome = function(s) {
   const len = s.length
   if(len===0) return ''
   const origin = s
   const reverse = s.split('').reverse().join('')
   // 初始化一维数组
   const dp = new Array(len).fill(0)
   dp[-1] = 0
   let maxLen = ''
   let lastIndex = null
   for (let i = 0; i < len; i++) {
     for (let j = len-1; j >= 0; j--) {
       if(origin[i]===reverse[j]){
         dp[j] = dp[j-1] + 1
         if(dp[j]>maxLen){
           // 判断下标是否对应
           const beforeRev = len - 1 - j
           if(beforeRev + dp[j] - 1 === i ){
             maxLen = dp[j]
             lastIndex = i
           }
         }
       }else dp[j] = 0
     }
   }
   const start = lastIndex - maxLen + 1
   return s.slice(start,start+maxLen)
 }

复杂度分析